The Efficient Test Theorem

When we are given a sequence of bits from a pseudo-random number generator, we often test the quality of the generator by doing things like counting the fraction of 0's, the fraction of subsequences of the form 111, etc.

A test is defined to be an efficiently computable function $T$ which takes as input a sequence of bits of length $m$ and gives as output a number between 0 and 1. Define

$$\begin{eqnarray*}A_r&=&\hbox{Average over all sequences $s$ }\{T(s)\}\\ A_g&=&\hbox{Average over $s$ from the generator }\{T(s)\}\end{eqnarray*}$$

These averages both involve finite operations-- $A_r$ involves adding up $T(s)$ over the $2^m$ possible $s$ and dividing. Similarly $A_g$ deals with an average over all possible seeds (presumably the number of possible seeds is much less than $2^m$).

It would take too much time to calculate $A_r,A_g$ exactly, but they can be estimated with high probability using the sampling ideas in section 7.3.

A generator is said to satisfy the test $T$ if $A_g$ is close to $A_r$, i. e., $T$ cannot tell the difference between sequences from the generator and genuinely random sequences. [we are being deliberately vague about the precise definition of ``close.'']

Theorem 30   If a generator satisfies the Next Bit Condition, it satisfies all efficiently computable tests $T$.

Proof: We will show that, if we had $T$ with $A_r$ significantly different from $A_g$, then for some $k$, $T$ could be used to predict the $(k+1)$-st bit from the first $k$ bits with probability somewhat larger than $1/2$. This would contradict the Next Bit Condition.

If $s$ is a sequence of $i$ bits, let $f_s$ be the fraction of all possible seeds whose first $i$ bits are $s$. For some $s$, we may have $f_s=0$. Note that

$$A_g=\sum_sf_sT(s)$$

where the sum is over all $s$ of length $m$.

The proof involves two steps:

1. Identify a $0\le k\le m-1$ such that the behavior of $T(s)$ depends in a significant way on the $(k+1)$-st bit of $s$.
2. Use $T$ to make a prediction for the $(k+1)$-st bit.

The proof of step 1 uses ideas similar to the ``sampling walk'' used to prove Theorem 5.1 in the Goldwasser-Micali paper. Define

$$A_i=\sum_{s,t}f_s2^{i-m}T(s\circ t)$$

where the sum is over all $s$ of length $i$ and $t$ of length $m-i$, with $\circ$ meaning to combine $s$ and $t$ to create a sequence of length $m$. $A_i$ is the expected value of $T$ applied to a sequence in which the first $i$ bits come from the generator (using a randomly chosen seed), with the remaining bits coming from a genuinely random source.

Note that $A_0=A_r$, $A_m=A_g$, and that all $A_i$ can be estimated with high probability using sampling. Since

$$\vert A_r-A_g\vert\le\sum_1^{m}\vert A_i-A_{i-1}\vert\hbox{ ... ...s $k$ with } \vert A_{k+1}-A_{k}\vert\ge \vert A_r-A_g\vert/m$$ (2)

This completes step 1.¹⁴

In step 2, we are concentrating on a specific sequence $s$ of length $k$, where $k$ satisfies (2). We wish to use the behavior of $T$ to predict whether the $(k+1)$-st bit should be 0 or 1. Intuitively, we ask $T$ which of the two possibilities would make the sequence look more random.

We will need to look at the analogues of the averages $A_k$ and $A_{k+1}$, restricting attention to those sequences which begin with $s$:

$$\begin{eqnarray*}A_k(s)&=&\sum_t2^{k-m}T(s\circ t)\\ A_{k+1}(s)&=&\sum_t(f_{s\c... ...0\circ t)+\\ &&\sum_t(f_{s\circ1}/f_s)2^{k+1-m}T(s\circ1\circ t)\end{eqnarray*}$$

The definition of $A_{k+1}(s)$ is based on the idea that $s\circ0$ and $s\circ1$ are the only sequences of length $k+1$ which begin with $s$. Note that, for $i=k$ or $k+1$, $A_i=\sum_sf_sA_i(s)$, where the sum is taken over all $s$ of length $k$.

$$\begin{eqnarray*}\hbox{Define\quad}A_{s,0}&=&\sum_t2^{k+1-m} T(s\circ0\circ t)\\ A_{s,1}&=&\sum_t2^{k+1-m}T(s\circ1\circ t)\end{eqnarray*}$$

These are the expected values of $T$ for a sequence which begins with $s$, has either 0 or 1 as its $(k+1)$-st term, and continues randomly. They can be estimated by sampling. Let $p_s$ be the fraction of the seeds which give $s$ as the first $k$ bits which give 0 as the $(k+1)-st$ bit (thus $p_s=f_{s\circ0}/f_s$). Then

$$A_k(s) = \frac{1}{2} A_{s,0}+ \frac{1}{2}A_{s,1}$$ (3)

$$A_{k+1}(s) = p_sA_{s,0}+(1-p_s)A_{s,1}$$ (4)

If we could estimate $p_s$ from (4), it would be simple to predict the next generated bit after $s$. Unfortunately, we cannot efficiently estimate $A_{k+1}(s)$. The problem is that we would have to sample among the seeds which generate $s$, and there is no easy way to find such seeds. Instead, we must find a way to use the information that the average of $A_{k+1}(s)$ is $A_{k+1}$, which we can estimate.

The (far from obvious) idea will be to have the prediction of the $(k+1)$-st bit itself be random. As we will see below, the probabilities can be assigned to the two possible predictions can be chosen so that the expected number of correct guesses looks like the right-hand side of (4).

We will assume $A_{k+1}>A_k$ [remember, we chose $k$ so that the difference between the two is significant]. The other case can be handled similarly. If $A_{s,0}>A_k(s)>A_{s,1}$, we would expect sequences beginning with $s\circ0$ to look more like things from the generator than sequences beginning with $s\circ1$. Our prediction for the next bit following $s$ will be random, given by

$${\renewedcommand{arraystretch}{1.2} \hbox{Predict }\left\{{}\... ...h probability $\frac{1}{2}+A_{s,1}-A_k(s)$\end{tabular}\right.}$$

[The probabilities add to 1 by equation (3).]

The probability that the prediction for input $s$ is correct is

$$\begin{eqnarray*}p_s\left(\frac{1}{2}+A_{s,0}-A_k(s)\right)+(1-p_s)\left( \frac{... ...p_sA_{s,0}+(1-p_s)A_{s,1} -A_k(s)&=&\frac{1}{2}+A_{k+1}(s)-A_k(s)\end{eqnarray*}$$

When we average over all seeds resulting in all possible $s$, we get a correct prediction with probability $1/2+A_{k+1}-A_k$, which, by (2), is significantly greater than $1/2$. ¹⁵

A consequence involving symmetry

The Next Bit Condition was stated in a way that clearly distinguished the beginning of the pseudo-random sequence from the end. By contrast, the Efficient Test Theorem treats a pseudo-random sequence in a completely symmetrical way. From that point of view, it does not matter which end of the sequence is used to start the construction. This leads to

Corollary 31   Let $n=pq$. Start with a random $1\le x\le n-1$ not divisible by $p$ or $q$. Let $a_0=x$, ${a_{i+1}}\equiv{a_i^2}\hbox{ (mod }{n})$. The sequence of bits given by $a_i$ mod 2 satisfies all efficient tests.

Footnotes

... 1.¹⁴

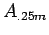Instead of estimating all the $A_i$, we could begin by estimating $A_{.5m}$. We would next estimate either $A_{.75m}$ or $A_{.25m}$, depending on whether $A_{.5m}$ was closer to $A_0$ or $A_m$.

.... ¹⁵

Thanks to R. Sengupta for pointing out the importance of the expression for $A_{k+1}(s)-A_k(s)$.