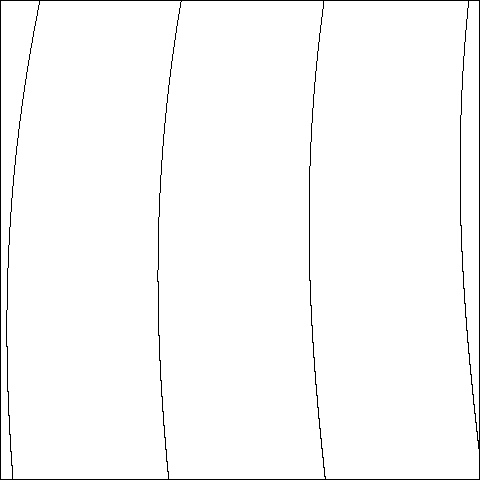
Parameter plane for P(x) = x3 - 3 a2 x +b , showing the window [0, 1.3] X [0, 1.3] in the (a, b)-plane.
STRETCHING RAYS, for the family of real cubic polynomials, are smooth
curves which fill out the region in parameter space where both critical
orbits escape to infinity. In the upper left hand region of the picture
above, these rays look like steep straight lines which seem to land
beautifully on the boundary curve. However NAKANE and KOMORI, making
essential use of complex methods, show that most of these rays actually
oscillate wildly, and accumulate on some entire interval of the real
analytic boundary curve. (REFERENCE: S. Nakane and Y. Komori, Tokyo
Institute of Polytechnics, to appear.) The pictures below try to illustrate
this.
DEFINITION: With the polynomial P(x) as above, the two critical points
a and -a are both real. If both orbits
{Pn(+-a) } tend to infinity, then
the ratio log|Pn(-a)|/log|Pn(a)| tends to a well defined limit L
as n tends to infinity. The STRETCHING RAYS can be described as the
level sets L = constant . (This is a very special case of a more
general construction of Branner and Hubbard.)
The parameter region in question is characterized by the property that the
graph of P lies above the diagonal everywhere to the right of the two
critical points. For parameters on the boundary curve, this graph just
touches the diagonal at one point.
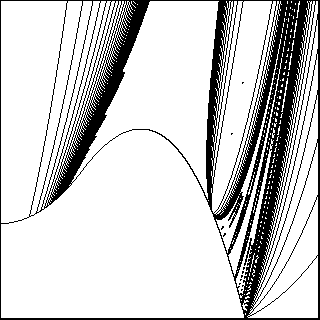
Here is a magnified picture of a small box in the parameter plane, showing that
the stretching rays are actually extremely wiggly:
Window [0.1, 0.1001] X [0.40235, 0.40245]
Here are pictures, showing stretching rays inside even smaller
boxes which get closer and closer to the smooth boundary curve:
Window [.1, .10001] X [.405, .40501]
Window [.1, .10001] X [.404, .40401]
Window [.1, .10001] X [.403, .40301]
Window [.1, .10001] X [.4027, .40271]
Window [.1, .10001] X [.40245, .40246]
Window [.1, .10001] X [.4024, .40241]
One can make similar pictures for the family of ``biquadratic maps''
P(x) = (x2 + a)2 + b , in the region of the parameter plane for which
the graph of P lies strictly above the diagonal.
Stony Brook, February 2000